จุดและเส้นตรง
แบบฝึกหัด
EASY
จุดและเส้นตรง
MEDIUM
จุดและเส้นตรง
HARD
จุดและเส้นตรง
เนื้อหา
จุดและเส้น
ระยะทางระหว่างจุดสองจุด
ระยะทางระหว่างจุด และ จุด
หาได้จาก

จุดกึ่งกลางระหว่างจุดสองจุด
ให้ เป็นจุดกึ่งกลางระหว่างจุด
และจุด
จะได้ว่า
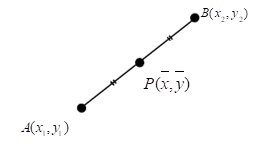
จุดแบ่งของส่วนของเส้นตรง
ให้ เป็นจุดบนส่วนของเส้นตรง
และ

โดยที่อัตราส่วน จะได้ว่า
จุดตัดกันของเส้นมัธยฐาน
ให้ และ
เป็นจุดยอดของรูปสามเหลี่ยม ABC โดยมี
เป็น จุดตัดของเส้นมัธยฐาน จะได้ว่า
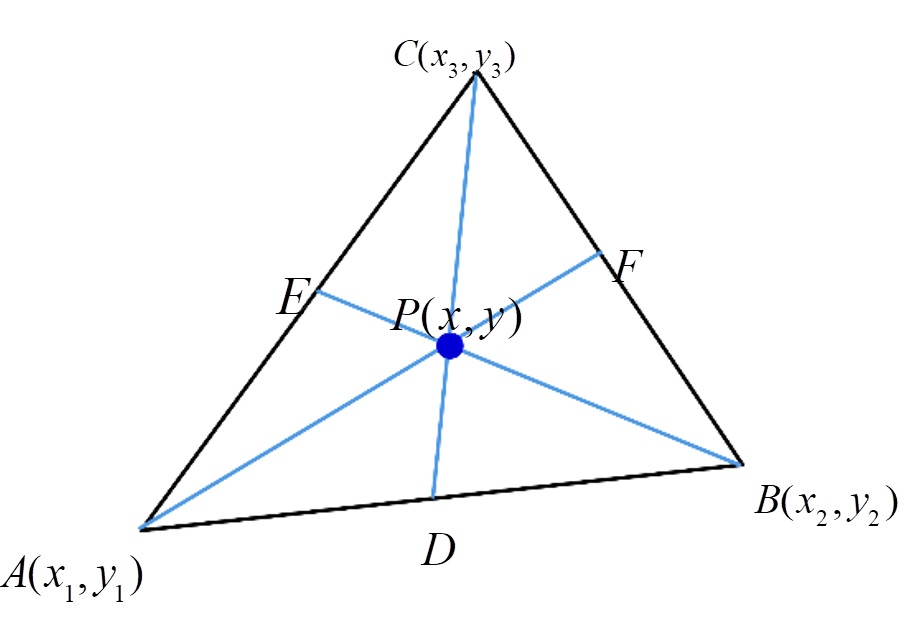
- โดย
พื้นที่ของรูปสามเหลี่ยม
ให้ และ
เป็นจุดยอดของรูปสามเหลี่ยม
จะได้ว่า
พื้นที่ของรูป
ระยะตัดแกนของเส้นตรง
ให้ เป็นเส้นตรงที่ตัดแกน
และ แกน
ณ จุดที่ห่างจากจุดกําเนิด เป็นระยะทางเท่ากับ
และ
ตามลําดับ ดังภาพ

เรียก ระยะตัดแกน
ของเส้นตรง
ถ้า แล้ว
ตัดแกน
ทางขวา
ถ้า แล้ว
ตัดแกน
ทางซ้าย
ความชันของเส้นตรง
ให้ แทนความชันของเส้นตรงที่ผ่านจุด
และ
แล้ว ความชันของเส้นตรงหาได้จาก

ลักษณะของเส้นตรงกับความชัน




สมการเส้นตรง
รูปมาตรฐาน เมื่อ
คือความชัน และ
คือ จุดตัดแกน
จะได้ ความชัน และ ระยะตัดแกน
ถ้า ผ่านจุด
และ
แล้ว สมการเส้นตรงหาได้จาก
ความสัมพันธ์ระหว่างเส้นตรง
ให้เส้นตรง มีสมการเป็น
และ เส้นตรง
มีสมการเป็น
เมื่อ และ
เป็นความชันของเส้นตรง
และ
ตามลําดับ จะได้ว่า
หรือ
และ
หาค่าไม่ได้
ระยะทางระหว่างจุดถึงเส้นตรง
ให้ เป็นระยะทางระหว่างจุด
ถึงเส้นตรง
จะได้ว่า

ระยะทางระหว่างเส้นคู่ขนาน
ให้ เป็นระยะทางระหว่างเส้นคู่ขนาน และ
มีสมการเป็น
มีสมการเป็น
จะได้ว่า

