กฎของโคไซน์และไซน์

สำหรับรูปสามเหลี่ยม $begin mathsize 14px style A B C end style$ ใด ๆ กำหนดให้ a, b และ c เป็นความยาวของด้านตรงข้ามมุม A, B และ C ตามลำดับ ดังรูป

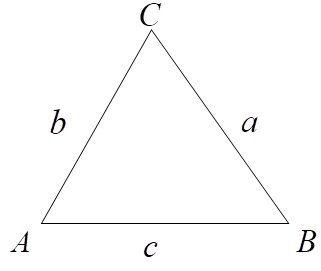
จะได้ ความสัมพันธ์ตามกฏของโคไซน์และไซน์ ดังนี้

กฎของโคไซน์

$a squared equals b squared plus c squared minus 2 b c space cos A b squared equals c squared plus a squared minus 2 a c space cos B c squared equals a squared plus b squared minus 2 a b space cos C$

จากกฎของโคไซน์ จะสังเกตได้ว่า

หากเราทราบขนาดมุมหนึ่งและความยาวด้านประกอบมุมนั้นแล้ว
เราจะสามารถหาความยาวด้านตรงข้ามมุมนั้นได้
หากเราทราบด้านทางสามด้านของสามเหลี่ยมใด ๆ
เราจะสามารถหาค่าโคไซน์ของมุมทั้งสามได้

กฏของไซน์

fraction numerator sin A over denominator a end fraction equals fraction numerator sin begin display style B end style over denominator b end fraction equals fraction numerator sin begin display style C end style over denominator c end fraction

จากกฎของไซน์ จะสังเกตได้ว่า

หากเราทราบไซน์ของมุม $2$ มุมในสามเหลี่ยมและทราบความยาวของด้านตรงข้ามมุมด้านหนึ่งจาก 2 มุมนั้นแล้ว เราสามารถหาความยาวของด้านตรงข้ามของอีกมุมหนึ่งได้
ถ้าเราทราบอัตราส่วนของไซน์ของมุมทั้งสามแล้ว เราจะสามารถหาอัตราส่วนของความยาวของด้านตรงข้ามมุมทั้งสามได้ และในทางกลับกัน หากเราทราบอัตราส่วนของความยาวของด้านตรงข้ามมุมทั้งสามแล้ว เราจะสามารถหาอัตราส่วนของค่าไซน์ของมุมทั้งสามได้เช่นกัน

กฎของโคไซน์และไซน์

แบบฝึกหัด

กฎของโคไซน์และไซน์ (ชุดที่ 1)

กฎของโคไซน์และไซน์ (ชุดที่ 2)

กฎของโคไซน์และไซน์ (ชุดที่ 3)

เนื้อหา

กฎของโคไซน์และไซน์

กฎของโคไซน์

กฏของไซน์

ทีมผู้จัดทำ

บทเรียน

ติดต่อเรา

ติดตามเรา

เราในสื่ออื่นๆ