ฟังก์ชันอื่นๆ ที่สำคัญ
แบบฝึกหัด
EASY
ฟังก์ชันเอกซ์โพเนนเชียล
EASY
ฟังก์ชันค่าสัมบูรณ์
EASY
ฟังก์ชันขั้นบันได
เนื้อหา
ฟังก์ชันอื่นๆ ที่สำคัญ
ฟังก์ชันนั้นมีอยู่หลายรูปแบบ แต่ละแบบก็มีการเรียกชื่อที่ไม่เหมือนกัน โดยหัวข้อก่อนหน้าเราได้ทำความรู้จักกับฟังก์ชันเส้นตรงและฟังก์ชันกำลังสองมาแล้ว แต่ยังมีฟังก์ชันอื่นๆ ที่สำคัญที่ควรรู้จัก ซึ่งในหัวข้อนี้กล่าวถึง ฟังก์ชันเอกซ์โพเนนเชียล ฟังก์ชันค่าสัมบูรณ์ และ ฟังก์ชันขั้นบันได
ฟังก์ชันเอกซ์โพเนนเชียล
ฟังก์ชันเอกซ์โพเนนเชียล คือ ฟังก์ชันที่อยู่ในรูป
ตัวอย่างที่ 1 กำหนดให้ ,
และ
จากฟังก์ชันที่กำหนด สามารถเขียนกราฟได้ดังนี้
จากตัวอย่างจะได้ว่า ลักษณะของกราฟฟังก์ชันเอกซ์โพเนนเชียลจะแบ่งเป็น 2 กรณี
| กรณีที่ 1 เมื่อ | กรณีที่ 2 เมื่อ |
 |  |
| เมื่อค่า เมื่อค่า | เมื่อค่า เมื่อค่า |
1. โดเมนของฟังก์ชันเอกโพเนนเชียลคือ
2. กราฟของฟังก์ชันเอกซ์โพเนนเชียลจะผ่านจุด
ฟังก์ชันค่าสัมบูรณ์
ฟังก์ชันค่าสัมบูรณ์ คือ ฟังก์ชันที่อยู่ในรูป
ตัวอย่างที่2 กำหนดให้ และ
จากฟังก์ชันที่กำหนด สามารถเขียนกราฟได้ดังนี้
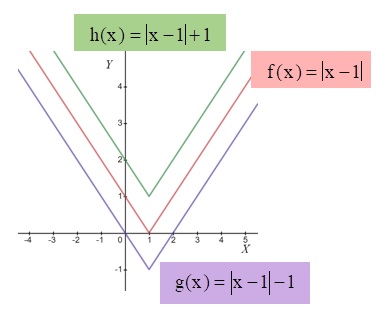
ตัวอย่างที่ 3 กำหนดให้
และ
จากฟังก์ชันที่กำหนด สามารถเขียนกราฟได้ดังนี้
- จากตัวอย่างเห็นว่า กราฟของฟังก์ชันค่าสัมบูรณ์มีลักษณะเป็นรูปตัววี และมีจุดยอดที่พิกัด
ฟังก์ชันขั้นบันได
ฟังก์ชันขั้นบันได คือ ฟังก์ชันที่มีโดเมนเป็นสับเซตของจำนวนจริง และมีค่าฟังก์ชันคงตัวเป็นช่วงๆ มากกว่า 2 ช่วง กราฟของฟังก์ชันนี้มีลักษณะคล้ายขั้นบันได ตัวอย่างเช่น