การแก้สมการและอสมการโดยใช้กราฟ

การแก้สมการกำลังสองโดยใช้กราฟ

การหาคำตอบของสมการกำลังสอง $a x squared plus b x plus c equals 0$ เมื่อ $a comma b comma c element of straight real numbers$ และ $a not equal to 0$ สามารถพิจารณาจากกราฟของฟังก์ชันกำลังสอง $y equals a x squared plus b x plus c$ ได้ โดยจุดที่กราฟตัดแกน $X$ เป็นจุดที่ $y equals 0$ และค่าของ ในพิกัดของ $x$ จุดตัดแกน $X$ ก็จะคือคำตอบของสมการ $a x squared plus b x plus c equals 0$ นั่นเอง เนื่องจากกราฟของฟังก์ชันกำลังสองมีลักษณะเป็นเส้นโค้งหงายหรือเส้นโค้งคว่ำทำให้กราฟแบ่งออกเป็น 3 ลักษณะดังนี้

1. กราฟไม่ตัดแกน X

กรณีนี้จะไม่มีคำตอบของ สมการ $a x squared plus b x plus c equals 0 comma a not equal to 0$ ที่เป็นจำนวนจริง ซึ่งจะสังเกตได้ว่าจะเกิดขึ้นเมื่อกราฟเป็นเส้นโค้งหงายและจุดวกกลับอยู่เหนือแกน $X$ (ฟังก์ชันจะอยู่ในรูป $y equals a open parentheses x minus h close parentheses squared plus k comma$ เมื่อ $a greater than 0$ และ $k greater than 0$ ) หรือ กราฟเป็นเส้นโค้งคว่ำและจุดวกกลับอยู่ใต้แกน $X$ (ฟังก์ชันจะอยู่ในรูป $y equals a open parentheses x minus h close parentheses squared plus k comma$ เมื่อ $a less than 0$ และ $k less than 0$ )

2. กราฟตัดแกน $X$ เพียงจุดเดียว

กรณีนี้สมการ $a x squared plus b x plus c equals 0 comma a not equal to 0$ จะมีคำตอบที่เป็นจำนวนจริงเพียงคำตอบเดียว ซึ่งจะสังเกตได้ว่าจะเกิดขึ้นเมื่อฟังก์ชันอยู่ในรูป $y equals a open parentheses x minus h close parentheses squared$ นั่นคือจะมีเพียงค่า $x equals h$ ที่จะทำให้ $y equals 0$

3. กราฟตัดแกน $X$ สองจุด

กรณีนี้สมการ $a x squared plus b x plus c equals 0 comma a not equal to 0$ จะมีคำตอบที่เป็นจำนวนจริงสองคำตอบ ซึ่งจะสังเกตได้ว่าจะเกิดขึ้นเมื่อกราฟเป็นเส้นโค้งหงายและจุดวกกลับอยู่ใต้แกน $X$ (ฟังก์ชันจะอยู่ในรูป $y equals a open parentheses x minus h close parentheses squared plus k comma$ เมื่อ $a greater than 0$ และ $k less than 0$ ) หรือ กราฟเป็นเส้นโค้งคว่ำและจุดวกกลับอยู่เหนือแกน $X$ (ฟังก์ชันจะอยู่ในรูป $y equals a open parentheses x minus h close parentheses squared plus k comma$ เมื่อ $a less than 0$ และ $k greater than 0$ )

การแก้อสมการกำลังสองโดยใช้กราฟ

นอกจากจะใช้กราฟช่วยในการหาคำตอบของสมการแล้ว เรายังสามารถใช้กราฟของฟังก์ชันกำลังสอง $y equals a x squared plus b x plus c comma a not equal to 0$ หาคำตอบของอสมการกำลังสองซึ่งอยู่ในรูป $a x squared plus b x plus c less than 0$ หรือ $a x squared plus b x plus c less or equal than 0$ หรือ $a x squared plus b x plus c greater than 0$ หรือ $a x squared plus b x plus c greater or equal than 0$ ได้อีกด้วย โดยการหาค่าของ $x$ ที่ทำให้ $y less than 0$ หรือ $y less or equal than 0$ หรือ $y greater than 0$ หรือ $y greater or equal than 0$ นั่นเอง

ตัวอย่างที่1 จากกราฟของฟังก์ชันกำลังสอง $y equals x squared minus 4$

วิธีทำ
จะเห็นได้ว่ากราฟตัดแกน $X$ สองจุดที่ $x equals negative 2$ และ $x equals 2$
โดยในช่วง $negative 2 less or equal than x less or equal than 2$ กราฟจะอยู่ใต้แกน $X$ นั่นคือ $y less or equal than 0$
ส่วน $x less or equal than negative 2$ หรือ $x greater or equal than 2$ กราฟจะอยู่เหนือแกน $X$ นั่นคือ $y greater or equal than 0$
จะได้ว่า $negative 2 less or equal than x less or equal than 2$ เป็นคำตอบของอสมการ $x squared minus 4 less or equal than 0$ และ
$x less or equal than negative 2$ หรือ $x greater or equal than 2$ เป็นคำตอบของอสมการ $x squared minus 4 greater or equal than 0$

ในการหาคำตอบของอสมการกำลังสองโดยใช้กราฟจะเริ่มจากการจัดรูปอสมการให้ด้านใดด้านหนึ่งเป็น 0 แล้วหาจุดตัดแกน $X$ ของฟังก์ชันกำลังสอง $y equals a x squared plus b x plus c$ ถ้าต้องการหาคำตอบของอสมการ $a x squared plus b x plus c less than 0$ หรือ $a x squared plus b x plus c less or equal than 0$ ให้หาช่วงของค่าที่ทำให้กราฟอยู่ใต้แกน $X$ และถ้าต้องการหาคำตอบของอสมการ $a x squared plus b x plus c greater than 0$ หรือ $a x squared plus b x plus c greater or equal than 0$ ให้หาช่วงของค่า $x$ ที่ทำให้กราฟอยู่เหนือแกน $X$ โดยช่วงของค่า $x$ จะถูกแบ่งโดยจุดตัดแกน $X$ นั่นเอง หรืออาจจะหาคำตอบของอสมการกำลังสองโดยแบ่งพิจารณา 2 ฟังก์ชันก็ได้ ดังตัวอย่างต่อไปนี้

ตัวอย่างที่2 จงหาคำตอบของอสมการ $x plus 4 greater than open parentheses x plus 1 close parentheses squared minus 3$

วิธีที่ 1
อสมการ $x plus 4 greater than open parentheses x plus 1 close parentheses squared minus 3$
สามารถจัดให้อยู่ในรูปอสมการ $x squared plus x minus 6 less than 0$
ให้ $y equals x squared plus x minus 6$
หาจุดตัดแกน $X$ ; $x squared plus x minus 6 equals 0$
$open parentheses x plus 3 close parentheses open parentheses x minus 2 close parentheses equals 0 x equals negative 3 comma 2$
จุดตัดแกน $X$ คือ $open parentheses negative 3 comma 0 close parentheses$ และ $open parentheses 2 comma 0 close parentheses$
พิจารณากราฟของ $y equals x squared plus x minus 6$ ซึ่งเป็นโค้งหงาย
จะได้ว่า $x squared plus x minus 6 less than 0 open parentheses y less than 0 close parentheses$ เมื่อ $negative 3 less than x less than 2$

ดังนั้น คำตอบของอสมการ $x plus 4 greater than open parentheses x plus 1 close parentheses squared minus 3$ คือ $negative 3 less than x less than 2$

วิธีที่ 2
จากอสมการ $x plus 4 greater than open parentheses x plus 1 close parentheses squared minus 3$
แบ่งพิจารณากราฟของ 2 ฟังก์ชัน คือ
$y equals x plus 4$ และ $y equals open parentheses x plus 1 close parentheses squared minus 3$
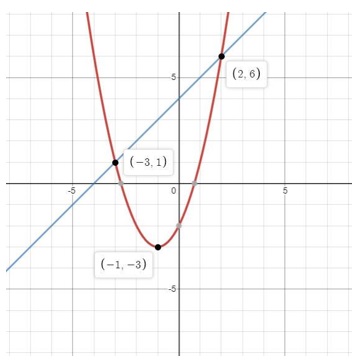
หาจุดตัดของกราฟทั้งสอง จาก $x plus 4 equals open parentheses x plus 1 close parentheses squared minus 3$
$x squared plus x minus 6 equals 0 open parentheses x plus 3 close parentheses open parentheses x minus 2 close parentheses equals 0 x equals negative 3 comma 2$

ซึ่งจะได้ว่ากราฟทั้งสองตัดกันที่จุด $open parentheses negative 3 comma 1 close parentheses$ และ $open parentheses 2 comma 6 close parentheses$
เมื่อพิจารณาจากกราฟ ค่าของฟังก์ชัน $y equals x plus 4$ จะมีค่ามากกว่าค่าของฟังก์ชัน $y equals open parentheses x plus 1 close parentheses squared minus 3$ เมื่อ $negative 3 less than x less than 2$

ดังนั้น คำตอบของอสมการ $x plus 4 greater than open parentheses x plus 1 close parentheses squared minus 3$ คือ $negative 3 less than x less than 2$

การแก้สมการและอสมการโดยใชักราฟ

แบบฝึกหัด

การแก้สมการและอสมการโดยใชักราฟ

การแก้สมการและอสมการโดยใชักราฟ

การแก้สมการและอสมการโดยใชักราฟ

เนื้อหา

การแก้สมการและอสมการโดยใช้กราฟ

การแก้สมการกำลังสองโดยใช้กราฟ

2. กราฟตัดแกน $X$ เพียงจุดเดียว

3. กราฟตัดแกน $X$ สองจุด

การแก้อสมการกำลังสองโดยใช้กราฟ

ทีมผู้จัดทำ

บทเรียน

ติดต่อเรา

ติดตามเรา

เราในสื่ออื่นๆ

การแก้สมการและอสมการโดยใชักราฟ

แบบฝึกหัด

การแก้สมการและอสมการโดยใชักราฟ

การแก้สมการและอสมการโดยใชักราฟ

การแก้สมการและอสมการโดยใชักราฟ

เนื้อหา

การแก้สมการและอสมการโดยใช้กราฟ

การแก้สมการกำลังสองโดยใช้กราฟ

2. กราฟตัดแกน เพียงจุดเดียว

3. กราฟตัดแกน สองจุด

การแก้อสมการกำลังสองโดยใช้กราฟ

ทีมผู้จัดทำ

บทเรียน

ติดต่อเรา

ติดตามเรา

เราในสื่ออื่นๆ

2. กราฟตัดแกน $X$ เพียงจุดเดียว

3. กราฟตัดแกน $X$ สองจุด