ความสัมพันธ์และฟังก์ชัน

เมื่อพิจารณาจำนวนนับสองจำนวน เช่น 2 กับ 8 เราอาจกล่าวได้ว่าจำนวนทั้งสองนี้เกี่ยวข้องกันโดย “2 มีค่าน้อยกว่า 8” หรือ “2 เป็นรากที่สามของ 8” คำว่า “น้อยกว่า” หรือ “เป็นรากที่สาม” คือคำที่ใช้แสดงความสัมพันธ์ระหว่างจำนวนทั้งสองนี้ได้ ดังนั้น ความสัมพันธ์ในทางคณิตศาสตร์จึงเกิดจากสิ่งสองสิ่งที่เกี่ยวข้องกันภายใต้กฎเกณฑ์อย่างใดอย่างหนึ่ง เราจึงสามารถใช้คู่อันดับแสดงความสัมพันธ์ระหว่างสมาชิกตัวหน้าและสมาชิกตัวหลังได้

นิยามความสัมพันธ์

คือ เซตของคู่อันดับซึ่งเป็นสับเซตของผลคูณคาร์ทีเซียนระหว่างเซต 2 เซต

ถ้ากำหนดให้

r

แทนความสัมพันธ์จากเซต

A

ไปยังเซต

B

จะได้ว่า

r subset of A cross times B

ถ้า

r subset of A cross times A

จะกล่าวว่า

r

เป็นความสัมพันธ์ใน

A

ตัวอย่างที่1 กำหนดให้ $A equals open curly brackets 1 comma 2 comma 3 comma 4 comma 5 comma 6 comma 7 close curly brackets$ และ $B equals open curly brackets 1 comma 2 comma 3 close curly brackets$

ถ้าให้ $r subscript 1$ เป็นความสัมพันธ์ “เป็นสองเท่า” จากเซต $A$ ไปยังเซต $B$ จะได้ $begin mathsize 14px style r subscript 1 equals open curly brackets open parentheses 2 comma 1 close parentheses comma open parentheses 4 comma 2 close parentheses comma open parentheses 6 comma 3 close parentheses close curly brackets subset of A cross times B end style$

ซึ่งในการเขียนแสดงความสัมพันธ์จะเขียนแบบแจกแจงสมาชิกหรือแบบบอกเงื่อนไขก็ได้ ความสัมพันธ์ $r subscript 1$ จึงสามารถเขียนแบบบอกเงื่อนไขได้ดังนี้
$begin mathsize 14px style r subscript 1 equals open curly brackets open parentheses x comma y close parentheses element of right enclose A cross times B space end enclose space x equals 2 y close curly brackets end style$

ในกรณีที่เซต $A$ และเซต $B$ เป็นเซตของจำนวนจริง เราจะสามารถเขียนเซตของความสัมพันธ์โดยละเว้นการเขียน $i cross times i$ ได้ เช่น
$r subscript 2 equals open curly brackets open parentheses x comma y close parentheses element of i cross times i space space left enclose space x equals 2 y end enclose close curly brackets space space space equals open curly brackets open parentheses x comma y close parentheses element of i cross times i space space left enclose space x equals 2 y end enclose close curly brackets$

นิยามโดเมน

นิยามโดเมน ของความสัมพันธ์ $r$ เขียนแทนด้วย $D subscript r$ คือ เซตของสมาชิกตัวหน้าในคู่อันดับของความสัมพันธ์ $r$ นั่นคือ

D subscript r equals open curly brackets x space space left enclose space open parentheses x comma y close parentheses element of r end enclose close curly brackets

เรนจ์

เรนจ์ ของความสัมพันธ์ $r$ เขียนแทนด้วย $R subscript 1$ คือ เซตของสมาชิกตัวหลังในคู่อันดับของความสัมพันธ์ $r$ นั่นคือ

R subscript r equals open curly brackets right enclose y space end enclose space open parentheses x comma y close parentheses element of r close curly brackets

จากตัวอย่างที่ 1 จะได้ $D subscript r subscript 1 end subscript equals open curly brackets 2 comma 4 comma 6 close curly brackets subset of A$ และ $R subscript r subscript 1 end subscript equals open curly brackets 1 comma 2 comma 3 close curly brackets subset of B$

ในการหาโดเมนของความสัมพันธ์ที่เขียนในรูปแบบบอกเงื่อนไขจะเขียน $y$ ให้อยู่ในรูปของ $x$ แล้วพิจารณาว่าค่า $x$ ใดบ้างที่ทำให้หาค่า $y$ ได้ เช่นเดียวกันกับการหาเรนจ์ก็จะเขียน $x$ ให้อยู่ในรูปของ $y$ แล้วพิจารณาว่าค่า $y$ ใดบ้างที่ทำให้หาค่า $x$ ได้ร่วมกับการพิจารณาโดเมน เช่น จาก $r subscript 2 equals open curly brackets right enclose open parentheses x comma y close parentheses space end enclose space x equals 2 y close curly brackets$ พิจารณา $y equals x over 2$ จะได้ $D subscript r subscript 2 end subscript equals straight real numbers$ และ $R subscript r subscript 2 end subscript equals straight real numbers$

ตัวอย่างที่ 2

กำหนดให้ $r subscript 3 equals open curly brackets right enclose open parentheses x comma y close parentheses space end enclose space y equals fraction numerator 1 over denominator square root of 2 x minus 1 end root end fraction close curly brackets$
จะได้ว่า $2 x minus 1 greater than 0$ และ $square root of 2 x minus 1 end root equals 1 over y greater than 0$
$D subscript r subscript 3 end subscript equals open curly brackets right enclose x space end enclose space x greater than 1 half close curly brackets$ และ $R subscript r subscript 3 end subscript equals open curly brackets right enclose y space end enclose space y greater than 0 close curly brackets$

นอกจากนี้การหาโดเมนและเรนจ์ของความสัมพันธ์สามารถพิจารณาจากกราฟของความสัมพันธ์ได้เช่นกัน

ตัวอย่างที่ 3

กำหนดให้ $r subscript 4 equals open curly brackets right enclose open parentheses x comma y close parentheses space end enclose space y equals 4 square root of 4 minus x squared end root close curly brackets$ ซึ่งกราฟของความสัมพันธ์นี้คือรูปครึ่งวงกลมที่มีรัศมีเท่ากับ 2 ดังรูป

เมื่อพิจารณาค่าของ $x$ และ $y$ จากกราฟ จะได้ว่า
$D subscript r subscript 4 end subscript equals open curly brackets right enclose x space end enclose space minus 2 less or equal than x less or equal than 2 close curly brackets$ และ $R subscript r subscript 4 end subscript equals open curly brackets right enclose y space end enclose space 0 less or equal than y less or equal than 2 close curly brackets$

ฟังก์ชัน

คือ ความสัมพันธ์ที่สมาชิกในโดเมนแต่ละตัวจับคู่กับสมาชิกในเรนจ์ของความสัมพันธ์เพียงตัวเดียวเท่านั้น

นิยาม ความสัมพันธ์ $r$ จากเซต $A$ ไปยังเซต $B$ จะเรียกว่าฟังก์ชัน ก็ต่อเมื่อ

D subscript r equals A

2. ถ้า

open parentheses x comma y close parentheses element of r

และ

open parentheses x comma z close parentheses element of r

แล้ว

y equals z

ตัวอย่างที่4
กำหนดให้ $A equals open curly brackets 1 comma 2 comma 3 comma 4 close curly brackets$ และ $B equals open curly brackets a comma b comma c close curly brackets$ พิจารณาความสัมพันธ์จากเซต $A$ ไปยังเซต $B$ ต่อไปนี้ว่าเป็นฟังก์ชันหรือไม่

1) $begin mathsize 14px style r subscript 5 equals open curly brackets open parentheses 1 comma a close parentheses comma open parentheses 2 comma a close parentheses comma open parentheses 3 comma b close parentheses comma open parentheses 3 comma c close parentheses comma open parentheses 4 comma a close parentheses close curly brackets end style$
ความสัมพันธ์ $r subscript 5$ ไม่เป็นฟังก์ชัน เพราะ $open parentheses 3 comma b close parentheses element of r subscript 5$ และ $open parentheses 3 comma c close parentheses element of r subscript 5$ แต่ $b not equal to c$

2) $r subscript 6 equals open curly brackets open parentheses 1 comma c close parentheses comma open parentheses 2 comma a close parentheses comma open parentheses 3 comma b close parentheses close curly brackets$
ความสัมพันธ์ $r subscript 6$ ไม่เป็นฟังก์ชัน เพราะ $D subscript r subscript 6 end subscript equals open curly brackets 1 comma 2 comma 3 close curly brackets not equal to A$

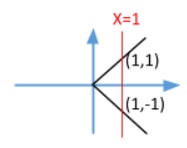
กรณีที่ความสัมพันธ์เขียนในรูปแบบบอกเงื่อนไข การพิจารณาการจับคู่ของสมาชิกตัวหน้าและสมาชิกตัวหลังของคู่อันดับอาจทำได้ยาก ในการพิจารณาว่าความสัมพันธ์ใดเป็นฟังก์ชันอาจจะพิจารณาจากกราฟของความสัมพันธ์นั้นได้เช่นกัน โดยการลากเส้นตรงขนานกับแกน $Y$ หากไม่มีเส้นตรงใดตัดกราฟของความสัมพันธ์ที่กำหนดมากกว่า 1 จุด ความสัมพันธ์นั้นจะเป็นฟังก์ชัน

ตัวอย่างที่ 5
กำหนดให้ $r subscript 7 equals open curly brackets right enclose open parentheses x comma y close parentheses space end enclose space x equals open vertical bar y close vertical bar close curly brackets$

พิจารณากราฟของความสัมพันธ์ $x equals open vertical bar y close vertical bar$

เมื่อลากเส้นตรง $x equals 1$ จะตัดกราฟ 2 จุด คือ จุด $open parentheses 1 comma 1 close parentheses$ และ $open parentheses 1 comma negative 1 close parentheses$

ความสัมพันธ์ $r subscript 1$ จึงไม่เป็นฟังก์ชัน เพราะ $open parentheses 1 comma 1 close parentheses element of r subscript 7$ และ $open parentheses 1 comma negative 1 close parentheses element of r subscript 7$ แต่ $1 not equal to negative 1$

ความสัมพันธ์และฟังก์ชัน

แบบฝึกหัด