การบวก ลบ เวกเตอร์ และการคูณด้วยสเกลาร์

การบวกเวกเตอร์ สามารถหาผลลัพธ์ ได้ดังนี้

1) วิธีหัวต่อหาง ให้นำเวกเตอร์มาเขียนต่อกัน โดยเอาหางลูกศรใหม่มาวางต่อที่หัวของลูกศรเดิม
ผลลัพธ์ที่ได้ คือ เวกเตอร์ที่ลากจากหางของเวกเตอร์แรกไปยังหัวของเวกเตอร์สุดท้าย

ตัวอย่าง กำหนดเวกเตอร์ ดังรูป

จะเขียนรูป เพื่อหาผลบวก $u with rightwards harpoon with barb upwards on top plus v with rightwards harpoon with barb upwards on top$ และ $mu with rightwards harpoon with barb upwards on top comma v with rightwards harpoon with barb upwards on top comma w with rightwards harpoon with barb upwards on top$ โดยวิธีหางต่อหัว ได้ดังนี้

จากรูป จะพบว่า ผลลัพธ์ของ $u with rightwards harpoon with barb upwards on top plus v with rightwards harpoon with barb upwards on top$ และ $u with rightwards harpoon with barb upwards on top comma v with rightwards harpoon with barb upwards on top comma w with rightwards harpoon with barb upwards on top$ ได้จากการลากเวกเตอร์จากหางของ
$u with rightwards harpoon with barb upwards on top$ ไปยังหัวของ $v with rightwards harpoon with barb upwards on top$ และจากหางของ $v with rightwards harpoon with barb upwards on top$ ไปยังหัวของ $w with rightwards harpoon with barb upwards on top$ ตามลำดับ

** สำหรับการบวกเวกเตอร์มากกว่า 2 เวกเตอร์ขึ้นไป สามารถทำได้ โดยการนำหัวมาต่อหางไปเรื่อย ๆ โดยผลลัพธ์สุดท้าย คือ เวกเตอร์ที่ได้จากการลากเชื่อมจากหางตัวแรกจนถึงหัวตัวสุดท้าย **

2) วิธีหางต่อหาง ให้นำหางของเวกเตอร์มาชนกัน แล้วลากเส้นประเพื่อสร้างให้เป็นรูปสี่เหลี่ยมด้านขนาน เส้นทแยงมุมของของสี่เหลี่ยมด้านขนานที่ได้ คือ ผลบวกของ $u with rightwards harpoon with barb upwards on top$ และ $v with rightwards harpoon with barb upwards on top$ ซึ่งวิธีการนี้อาจเรียกอีกอย่างหนึ่งว่า

“ วิธีสร้างรูปปิดของสี่เหลี่ยมด้านขนาน ”

ตัวอย่าง กำหนดเวกเตอร์ ดังรูป

จะเขียนรูป เพื่อหาผลบวก $u with rightwards harpoon with barb upwards on top plus v with rightwards harpoon with barb upwards on top$ โดยวิธีหางต่อหาง ได้ดังนี้

สมบัติของการบวกเวกเตอร์

1) สมบัติปิด (เวกเตอร์บวกกัน ผลลัพธ์ที่ได้ จะเป็นเวกเตอร์เสมอ)

2) สมบัติการสลับที่ $u with rightwards harpoon with barb upwards on top comma v with rightwards harpoon with barb upwards on top equals v with rightwards harpoon with barb upwards on top plus u with rightwards harpoon with barb upwards on top$

3) สมบัติการเปลี่ยนกลุ่ม $open parentheses u with rightwards harpoon with barb upwards on top plus v with rightwards harpoon with barb upwards on top close parentheses plus w with rightwards harpoon with barb upwards on top space equals u with rightwards harpoon with barb upwards on top plus open parentheses v with rightwards harpoon with barb upwards on top comma w with rightwards harpoon with barb upwards on top close parentheses$

4) เอกลักษณ์การบวกของเวกเตอร์ คือ เวกเตอร์ศูนย์ $open parentheses 0 with rightwards harpoon with barb upwards on top close parentheses$
ซึ่งเป็นเวกเตอร์ที่มีขนาด 0 หน่วย นั่นคือ $u with rightwards harpoon with barb upwards on top plus 0 with rightwards harpoon with barb upwards on top equals 0 with rightwards harpoon with barb upwards on top plus u with rightwards harpoon with barb upwards on top equals u with rightwards harpoon with barb upwards on top$

5) อินเวอร์สการบวกของเวกเตอร์ $u with rightwards harpoon with barb upwards on top$ เขียนสัญลักษณ์ว่า $negative u with rightwards harpoon with barb upwards on top$
(หมายถึง เวกเตอร์ที่มีขนาดเท่ากัน แต่มีทิศทางตรงกันข้ามกับเวกเตอร์ $u with rightwards harpoon with barb upwards on top$ )
นั่นคือ $u with rightwards harpoon with barb upwards on top plus open parentheses negative u with rightwards harpoon with barb upwards on top close parentheses equals 0 with rightwards harpoon with barb upwards on top equals open parentheses negative u with rightwards harpoon with barb upwards on top close parentheses plus u with rightwards harpoon with barb upwards on top$

การลบเวกเตอร์

เราสามารถหาผลลบของเวกเตอร์ได้ โดยใช้หลักการเดียวกับการบวกเวกเตอร์
(สามารถใช้ได้ทั้งวิธีหัวต่อหาง หรือ วิธีหางต่อหาง ก็ได้)
โดยเราจะมอง $u with rightwards harpoon with barb upwards on top minus v with rightwards harpoon with barb upwards on top equals u with rightwards harpoon with barb upwards on top plus open parentheses negative v with rightwards harpoon with barb upwards on top close parentheses$ ซึ่งก็คือ ผลบวกของ $u with rightwards harpoon with barb upwards on top$ และ $v with rightwards harpoon with barb upwards on top$ (เวกเตอร์ตรงข้ามของ $v with rightwards harpoon with barb upwards on top$ )

ตัวอย่าง กำหนดเวกเตอร์ ดังรูป

สามารถเขียนรูป เพื่อหาผลลบของ $u with rightwards harpoon with barb upwards on top minus v with rightwards harpoon with barb upwards on top$ ได้ดังนี้

** กล่าวโดยสรุป วิธีการหาผลบวกและผลลบของเวกเตอร์โดยวิธีหางต่อหาง คือ การนำหางเวกเตอร์มาชนกัน แล้วลากเส้นประให้เป็นรูปสี่เหลี่ยมด้านขนาน จะได้ว่า เส้นทแยงมุมเส้นหนึ่งเป็นผลบวก (พุ่งออกจากมุมที่หางชนกัน) และเส้นทแยงมุมอีกเส้นหนึ่งเป็นลบ (เชื่อมระหว่างหัวลูกศร)
ดังรูป

** มุม $straight theta$ ระหว่าง $u with rightwards harpoon with barb upwards on top$ กับ $v with rightwards harpoon with barb upwards on top$ ต้องวัดระหว่างหางชนหางเสมอ และต้องมีขนาดไม่เกิน $180 degree$ **

การคูณเวกเตอร์ด้วยสเกลาร์

ให้ $a$ เป็นสเกลาร์ และ $u with rightwards harpoon with barb upwards on top$ เป็นเวกเตอร์ ผลคูณของเวกเตอร์ $u with rightwards harpoon with barb upwards on top$ ด้วยสเกลาร์ $a$ เป็นเวกเตอร์
เขียนแทนด้วย $a u with rightwards harpoon with barb upwards on top$ โดยที่

1) ถ้า $a equals 0$ จะได้ว่า $a u with rightwards harpoon with barb upwards on top equals 0 with rightwards harpoon with barb upwards on top$

2) ถ้า $a greater than 0$ จะได้ว่า $a u with rightwards harpoon with barb upwards on top$ เป็นเวกเตอร์ที่มีทิศเดียวกันกับ $u with rightwards harpoon with barb upwards on top$ และมีขนาดเท่ากับ $open vertical bar a close vertical bar times open vertical bar u with rightwards harpoon with barb upwards on top close vertical bar$

3) ถ้า $a less than 0$ จะได้ว่า $a u with rightwards harpoon with barb upwards on top$ เป็นเวกเตอร์ที่มีทิศตรงข้ามกับ $u with rightwards harpoon with barb upwards on top$ และมีขนาดเท่ากับ $open vertical bar a close vertical bar times open vertical bar u with rightwards harpoon with barb upwards on top close vertical bar$

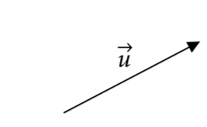
ตัวอย่าง กำหนดเวกเตอร์ $u with rightwards harpoon with barb upwards on top$ ดังรูป

จะได้ เวกเตอร์ $2 over 3 u with rightwards harpoon with barb upwards on top$ และ $negative 0.75 u with rightwards harpoon with barb upwards on top$ เป็น ดังนี้

ทิศทางเดิม แต่ขนาดลดลงเหลือ 2 ใน 3 ของเวกเตอร์ $u with rightwards harpoon with barb upwards on top$
ทิศตรงกันข้าม ขนาดเป็น 0.75 เท่าของเวกเตอร์ $u with rightwards harpoon with barb upwards on top$

สมบัติการคูณเวกเตอร์ด้วยสเกลาร์

ให้ $a comma b$ เป็นสเกลาร์ และ $u with rightwards harpoon with barb upwards on top comma v with rightwards harpoon with barb upwards on top$ เป็นเวกเตอร์ จะได้ว่า

1) $a u with rightwards harpoon with barb upwards on top$ เป็นเวกเตอร์

2) $a open parentheses b u with rightwards harpoon with barb upwards on top close parentheses equals open parentheses a b close parentheses u with rightwards harpoon with barb upwards on top$ : สมบัติการเปลี่ยนกลุ่ม

3) $open parentheses a plus b close parentheses u with rightwards harpoon with barb upwards on top equals a u with rightwards harpoon with barb upwards on top plus b u with rightwards harpoon with barb upwards on top$ และ $a open parentheses u with rightwards harpoon with barb upwards on top plus v with rightwards harpoon with barb upwards on top close parentheses equals a u with rightwards harpoon with barb upwards on top plus a v with rightwards harpoon with barb upwards on top$ : สมบัติการแจกแจง

4) $1 u with rightwards harpoon with barb upwards on top equals u with rightwards harpoon with barb upwards on top$

ความสัมพันธ์ระหว่างการคูณเวกเตอร์ด้วย
สเกลาร์กับการขนานกัน

กำหนดให้ $u with rightwards harpoon with barb upwards on top not equal to 0 with rightwards harpoon with barb upwards on top$ และ $v with rightwards harpoon with barb upwards on top not equal to 0 with rightwards harpoon with barb upwards on top$ จะได้ว่า

1) ถ้า $u with rightwards harpoon with barb upwards on top$ ขนานกับ $v with rightwards harpoon with barb upwards on top$ แล้ว จะมีจำนวนจริง $k$   ซึ่ง $k not equal to 0$   ที่ทำให้ $u with rightwards harpoon with barb upwards on top equals k v with rightwards harpoon with barb upwards on top$
โดยพิจารณาจากค่า   ดังนี้
1.1)   ถ้า $k greater than 0$   ; $u with rightwards harpoon with barb upwards on top$ และ $v with rightwards harpoon with barb upwards on top$ จะขนานกัน และมีทิศทางเดียวกัน
1.2)   ถ้า $k less than 0$    ; $u with rightwards harpoon with barb upwards on top$ และ $v with rightwards harpoon with barb upwards on top$ จะขนานกัน และมีทิศทางตรงกันข้าม

2) ถ้า $u with rightwards harpoon with barb upwards on top$ ไม่ขนานกับ $v with rightwards harpoon with barb upwards on top$ และ $a u with rightwards harpoon with barb upwards on top plus b v with rightwards harpoon with barb upwards on top equals 0 with rightwards harpoon with barb upwards on top$ แล้ว $a equals 0$ และ $b equals 0$

ตัวอย่าง กำหนดให้ $u with rightwards harpoon with barb upwards on top comma v with rightwards harpoon with barb upwards on top not equal to 0 with rightwards harpoon with barb upwards on top$ และ $open parentheses x squared minus 5 close parentheses u with rightwards harpoon with barb upwards on top minus v with rightwards harpoon with barb upwards on top equals open parentheses 1 minus x close parentheses stack u minus 3 v with rightwards harpoon with barb upwards on top with rightwards harpoon with barb upwards on top$

จงหาค่า $x$ ที่ทำให้ $u with rightwards harpoon with barb upwards on top$ ขนานกับ $v with rightwards harpoon with barb upwards on top$
จากสมการ $open parentheses x squared minus 5 close parentheses u with rightwards harpoon with barb upwards on top minus v with rightwards harpoon with barb upwards on top equals open parentheses 1 minus x close parentheses u with rightwards harpoon with barb upwards on top minus 3 v with rightwards harpoon with barb upwards on top$
จะได้ว่า     $open parentheses x squared minus 5 minus 1 plus x close parentheses u with rightwards harpoon with barb upwards on top equals negative 2 v with rightwards harpoon with barb upwards on top$
เนื่องจาก $u with rightwards harpoon with barb upwards on top$ ขนานกับ $v with rightwards harpoon with barb upwards on top$ แสดงว่า   $x squared minus 5 minus 1 plus x not equal to 0$
นั่นคือ $x squared plus x minus 6 not equal to 0$      แยกตัวประกอบได้ $open parentheses x plus 3 close parentheses open parentheses x minus 2 close parentheses not equal to 0$
เพราะฉะนั้น $x not equal to 0 comma negative 3 comma 2$

ดังนั้น ค่า $x$ ที่ทำให้ $u with rightwards harpoon with barb upwards on top$ ขนานกับ $v with rightwards harpoon with barb upwards on top$ คือ $x element of straight real numbers minus open curly brackets negative 3 comma 2 close curly brackets$

จงหาค่า $x$ ที่ทำให้ $u with rightwards harpoon with barb upwards on top$ มีทิศทางเดียวกับ $v with rightwards harpoon with barb upwards on top$

จากสมการ $open parentheses x squared minus 5 close parentheses u with rightwards harpoon with barb upwards on top minus v with rightwards harpoon with barb upwards on top equals open parentheses 1 minus x close parentheses u with rightwards harpoon with barb upwards on top minus 3 v with rightwards harpoon with barb upwards on top$
จะได้ว่า $open parentheses x squared minus 5 minus 1 plus x close parentheses u with rightwards harpoon with barb upwards on top equals negative 2 v with rightwards harpoon with barb upwards on top$

จะพบว่า สัมประสิทธิ์หน้า $v with rightwards harpoon with barb upwards on top$ เป็นค่าติดลบ
ดังนั้น ถ้า $u with rightwards harpoon with barb upwards on top$ มีทิศทางเดียวกับ $v with rightwards harpoon with barb upwards on top$ ได้
สัมประสิทธิ์หน้า $u with rightwards harpoon with barb upwards on top$ จะต้องติดลบด้วย
แสดงว่า   $x squared minus 5 minus 1 plus x less than 0$
นั่นคือ $x squared plus x minus 6 less than 0$
แยกตัวประกอบได้ $open parentheses x plus 3 close parentheses open parentheses x minus 2 close parentheses less than 0$
เพราะฉะนั้น $negative 3 less than x less than 2$

ดังนั้น ค่า $x$ ที่ทำให้ $u with rightwards harpoon with barb upwards on top$ มีทิศทางเดียวกับ $v with rightwards harpoon with barb upwards on top$ คือ $x element of open parentheses negative 3 comma 2 close parentheses$

** หมายเหตุ ** ถ้าเปลี่ยนโจทย์เป็น $u with rightwards harpoon with barb upwards on top$ มีทิศทางตรงข้ามกับ $v with rightwards harpoon with barb upwards on top$ แสดงว่า สัมประสิทธิ์หน้า $u with rightwards harpoon with barb upwards on top$ จะต้อง เป็นค่าบวก แสดงว่า $x squared minus 5 minus 1 plus x greater than 0$ นั่นคือ $x squared plus x minus 6 greater than 0$
แยกตัวประกอบได้ $open parentheses x plus 3 close parentheses open parentheses x minus 2 close parentheses greater than 0$

ดังนั้น ค่า $x$ ที่ทำให้ $u with rightwards harpoon with barb upwards on top$ มีทิศทางตรงข้ามกับ $v with rightwards harpoon with barb upwards on top$ คือ $x element of open parentheses negative infinity comma negative 3 close parentheses union open parentheses 2 comma infinity close parentheses$

การบวก ลบ เวกเตอร์ และคูณด้วยสเกลาร์

แบบฝึกหัด

การบวกลบเวกเตอร์และคูณด้วยสเกลาร์

การบวกลบเวกเตอร์และคูณด้วยสเกลาร์

การบวกลบเวกเตอร์และคูณด้วยสเกลาร์

เนื้อหา

การบวก ลบ เวกเตอร์ และการคูณด้วยสเกลาร์

สมบัติของการบวกเวกเตอร์

การลบเวกเตอร์

การคูณเวกเตอร์ด้วยสเกลาร์

สมบัติการคูณเวกเตอร์ด้วยสเกลาร์

ความสัมพันธ์ระหว่างการคูณเวกเตอร์ด้วย
สเกลาร์กับการขนานกัน

ทีมผู้จัดทำ

บทเรียน

ติดต่อเรา

ติดตามเรา

เราในสื่ออื่นๆ

การบวก ลบ เวกเตอร์ และคูณด้วยสเกลาร์

แบบฝึกหัด

การบวกลบเวกเตอร์และคูณด้วยสเกลาร์

การบวกลบเวกเตอร์และคูณด้วยสเกลาร์

การบวกลบเวกเตอร์และคูณด้วยสเกลาร์

เนื้อหา

การบวก ลบ เวกเตอร์ และการคูณด้วยสเกลาร์

สมบัติของการบวกเวกเตอร์

การลบเวกเตอร์

การคูณเวกเตอร์ด้วยสเกลาร์

สมบัติการคูณเวกเตอร์ด้วยสเกลาร์

ความสัมพันธ์ระหว่างการคูณเวกเตอร์ด้วยสเกลาร์กับการขนานกัน

ทีมผู้จัดทำ

บทเรียน

ติดต่อเรา

ติดตามเรา

เราในสื่ออื่นๆ

ความสัมพันธ์ระหว่างการคูณเวกเตอร์ด้วย
สเกลาร์กับการขนานกัน